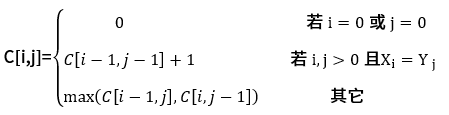求解两个长度为n的序列X和Y的一个最长公共子序列(如序列ABCBDAB和BDCABA的一个最长公共子序列为BCBA)可以采用多种计算方法。如可以采用蛮力法,对X的每一个子序列,判断其是否也是Y的子序列,最后求出最长的即可,该方法的时间复杂度为( )。经分析发现该问题具有最优子结构,可以定义序列长度分别为i和j的两个序列X和Y的最长公共子序列的长度为C[i,j],如下式所示。
采用自底向上的方法实现该算法,则时间复杂度为( )。
问题1选项
A.O(n²)
B.O(n²lgn)
C.O(n³)
D.O(n2
n)
问题2选项
A.O(n²)
B.O(n²lgn)
C.O(n³)
D.O(n2
n)
第1题:1.X、Y的所有子序列都检查过后即可求出X、Y的最长公共子序列。X的一个子序列相应于下标序列1,2,…,n的一个子序列。因此,X共有2n个子序列。当然,Y也有2m个子序列。判断一个子序列是否也是Y的子序列的时间是n,因此时间复杂度为O(n2n)
2. 动态规划的一个计算最长公共子序列的方法如下,两个序列 X、Y :
设有二维数组 c[i][j] 表示 X 的 i 位和 Y 的 j 位之前的最长公共子序列的长度,则有题干给定的函数表现形式:
其中,c(i,j)当 X 的第i位与 Y 的第 j 位完全相同时为“1” ,否则为“0” 。
此时,c[i][j]中最大的数便是 X 和 Y 的最长公共子序列的长度,依据该数组回溯,便可找出最长公共子序列。该算法的空间、时间复杂度均为O(n2)。
''
第2题: