第1题:
本题是项目管理中,时间管理的关键路径问题。先将题目中的各个节点依赖关系画出来,如图所示:
通过节点依赖图,结合题目正常进度所需天数很容易看出ACD为关键路径。关键路径长度为12天。但这样得到的就是最短工期与最少花费吗?不是。因为题目指出间接花费是每天5万元,而赶工每天的费用仅2-4万。此时赶工完成部分任务,既能缩短工期,又能降低费用,是合适的解决方案,经过分析,赶工方案为:
A赶工2天,B赶工1天,D赶工3天。此时关键路径长度为7天,总花费为106万。
分析过程如下:
(1)总成本=直接成本+间接成本。
赶工处理之前,项目的直接成本是各个作业的直接费用10+15+12+18=55万元;
间接费用,根据题干“该工程的间接费用为每天5万元”,项目工期为12天,所以间接成本是12×5=60万元;
总成本=55+60=115万元。
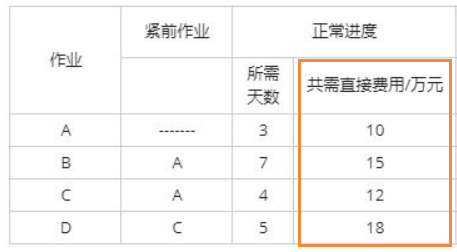
(2)赶工的必要性:每压缩一天工期,可以节约间接成本5万元,而赶工每天会增加直接成本,只要赶工增加的成本不超过5万元,那么就可以安排赶工,节约项目总成本。
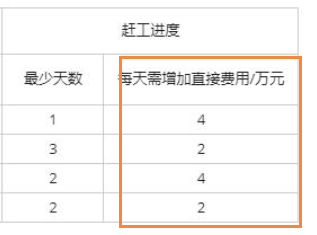
(3)确定赶工方案:赶工必定是节约了间接成本,也就是压缩了项目工期,只有关键路径才能影响项目工期。
根据关键路径A-C-D(12天),选择代价最小的作业进行压缩,也就是D活动,当D活动压缩2天之后,A-C-D工期为10天,与A-B工期一样;
此时关键路径发生了改变,有2条关键路径,分别是A-C-D和A-B,此时若要压缩工期,必须2条路径同时压缩,那么此时的压缩方案有多种:压缩相交节点A,每天增加直接成本4万元;同时压缩B和D,每天增加成本2+2=4万。由于A原本需要3天最少需要1天,可压缩的空间是2天,B活动原本需要7天最少需要3天,可压缩空间4天,D活动原本需要5天最少需要2天,可压缩空间是3天,之前已经对D压缩了2天,也就是说B和D同时压缩的方案,由于D的限制,还有1天可压缩。
此时可压缩方案分别是A压缩2天,B和D同时压缩1天,项目工期为10-2-1=7天。
综上:赶工的全部过程如下,(1)D压缩2天;(2)A压缩2天;(3)B和D压缩1天。(其中(2)和(3)顺序可交换)。
也就是A压缩2天,B压缩1天,D压缩3天。
(4)确定最终的花费:
间接成本:7×5=35万元
直接成本:原直接费用10+15+12+18=55万元,赶工费用,A:4×2=8;B:2×1=2;D:2×3=6;总直接成本:55+8+2+6=71万元
总成本:35+71=106万元。
'
第2题: