试题出自试卷《2009年下半年系统架构设计师考试上午真题（专业解析+参考答案）》

问题1选项
A.AB
B.DE
C.CE
D.DB

问题2选项
A.p=｛R1(AC)，R2(ED)，R3(B)｝
B.p=｛R1(AC)，R2(E)，R3(DB)｝
C.p=｛R1(AC)，R2(ED)，R3(AB)｝
D.p=｛R1(ABC)，R2(ED)，R3(ACE)｝

第1题:C

第2题:D

第1题:本题考查如何求解候选关键字和对模式分解知识的掌握。
给定一个关系模式R(U，F)，U={A₁，A₂，...，A_n}，F是R的函数依赖集，若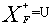=U，则X必为R的唯一候选关键字。对于试题（7），A选项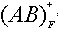=ABD≠U，所以AB非候选关键字；B选项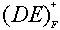=ABDE≠U，所以DE非候选关键字；C选项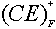=ABCDE=U，所以CE为候选关键字；D选项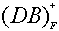=BD≠U，所以DB非候选关键字。
根据无损连接的判定算法，对选项A构造初始的判定表如下：
　　由于A→B，DE→B，CB→E，E→A，B→D的决定因素中没有两行是相同的，因此选项A是有损连接的。
　　对选项B构造初始的判定表如下：

由于A→B，DE→B，CB→E， E→A， B→D的决定因素中没有两行是相同的，因此选项B是有损连接的。
对选项C构造初始的判定表如下：

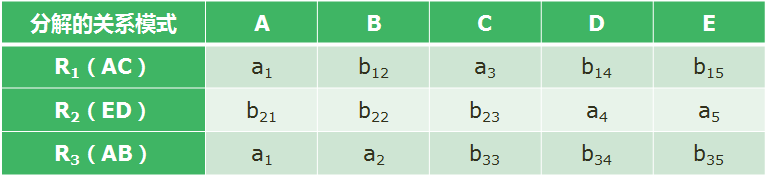
由于A→B，属性A的第1行和第3行相同，可以将第1行b ₁₂改为a ₂；又由于B→D，属性B的第1行和第3行相同，而属性D第1行b ₁₄和第3行b ₃₄改为a ₄，因此改为同一符号，即取行号值最小的b ₁₄。修改后的判定表如下：

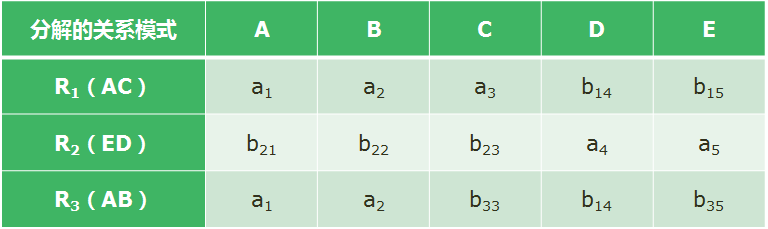
反复检查函数依赖集F，无法修改上表，所以选项C是有损连接的。
对选项D构造初始的判定表如下：

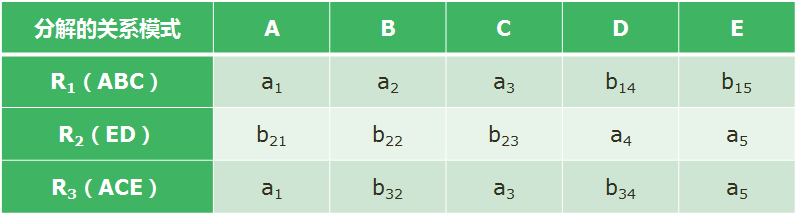
由于A→B，属性A的第1行和第3行相同，可以将第3行b ₃₂改为a ₂ ；E→A，属性E的第2行和第3行相同，可以将属性A第2行b ₂₁改为a _l ；AC→E，属性E的第2行和第3行相同，可以将属性E第1行b ₁₅改为a ₅ ；B→D，属性B的第1行和第3行相同，属性D第1行b ₁₄和第3行b ₃₄没有一行为a ₄，因此改为同一符号，即取行号值最小的b ₁₄。修改后的判定表如下：

E→D，属性E的第1～3行相同，可以将属性D第1行b ₁₄和第3行b ₃₄改为a ₄。修改后的判定表如下：

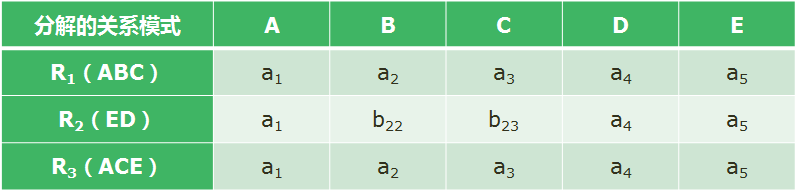
由于上表第一行全为a，故分解无损。
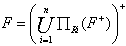
现在分析该分解是否保持函数依赖。若分解保持函数依赖，那么分解的子模式的函数依赖集 。F _R1=A→B， CB→A，F _R2=E→D（根据Armstrong公理，系统传递依赖，E→A， A→B， B→D，所以E→D），F _R3=E→A。可以求证F ⁺与(F _R1+F _R2+F _R3) ⁺等价，即F ⁺=(F _R1+F _R2+F _R3) ⁺=(A→B，CB→A，E→D，E→A) ⁺，所以该分解保持函数依赖。'''''

第2题: