已知矩阵Am*n和Bn*p相乘的时间复杂度为O(mnp)。矩阵相乘满足结合律,如三个矩阵A、B、C相乘的顺序可以是(A*B)*C也可以是A*(B*C)。不同的相乘顺序所需进行的乘法次数可能有很大的差别。因此确定n个矩阵相乘的最优计算顺序是一个非常重要的问题。已知确定n个矩阵A1A2......An相乘的计算顺序具有最优子结构,即A1A2......An的最优计算顺序包含其子问题A1A2......Ak和Ak+1Ak+2……An(1≤k)的最优计算顺序。
可以列出其递归式为:
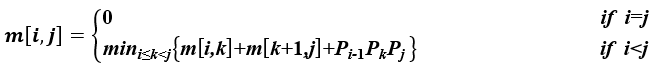
其中,Ai的维度为pi-1*pi,m[i,j]表示AiAi+1……Aj最优计算顺序的相乘次数。
先采用自底向上的方法求n个矩阵相乘的最优计算顺序。则求解该问题的算法设计策略为( )。算法的时间复杂度为( ),空间复杂度为( )。
给定一个实例,(p0p1……p5)=(20,15,4,10,20,25),最优计算顺序为( )。
第1题:
本题考查算法设计与分析-动态规划知识。
第一空:本题提到“已知确定n个矩阵A1A2......An相乘的计算顺序具有最优子结构,即A1A2......An的最优计算顺序包含其子问题A1A2......Ak和Ak+1Ak+2……An(1≤k)的最优计算顺序”,即规模为n的问题的解与较小规模为k的问题的解有关,具有最优子结构,并且提到“m[i,j]表示AiAi+1……Aj最优计算顺序的相乘次数”即,用中间数组m[i,j]存放中间子结果,所以本题描述的算法策略是动态规划法,特点是具有最优子结构,并且会利用中间表记录中间结果,最后利用查表得到最优解。
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独 立且与原问题性质相同。
贪心在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解 。
回溯法是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择 。
第2题:
第二空:题干给出“已知矩阵Am*n和Bn*p相乘的时间复杂度为O(mnp)”,即矩阵乘法的实现过程,可以简单理解为3层嵌套循环,所以时间复杂度为O(n^3)。
下面给出一个简单的矩阵乘法的代码段(只列出动态规划过程,具体变量声明已忽略):
int cmm(int n,int p[]){
//n为矩阵个数,p[]为维度记录,本题n=5,p[]={20,15,4,10,20,25}
for(t=1;t < n;t++){
for(i=0;i < n-t;i++){
j=i+t;
tempCost = -1;
for(k=i;k < j;k++){
temp=m[i][k]+m[k+1][j]+p[i]*p[k]*p[j];
//此处由p[]数组从0开始记录,i下标无需减1,原公式Pi-1*Pk*Pj转换为p[i]*p[k]*p[j]即可
if(tempCost==-1||tempCost > temp){
tempCost=temp;
tempTrace=k;
}
}
m[i][j]=tempCost; //m[][]:二维数组,长度为n×n,此处数组从0开始记录,矩阵A的i、j、k下标无需减1,用m[i][j]表示 Ai+1Ai+2…Aj+1 的最优计算的计算代价
trace[i][j]=tempTrace; // trace[][]:二维数组,长度为n*n,其中元素trace[i][j]表示Ai+1*Ai+2*Aj+1的最优计算对应的划分位置,即k。
}
}
return m[0][n-1]; //返回值为最优计算的计算代价,即乘法的次数
}
''''
第3题:
第三空:本题在计算过程中,需要临时存储空间存放中间结果m[][],二维数组占据空间为n*n,即空间复杂度为O(n^2)。
第4题:
第四空:可以按照选项直接计算出相应乘法次数进行判断。
给定一个实例,(p0p1……p5)=(20,15,4,10,20,25), 表示A1(20×15),A2(15×4),A3(4×10),A4(10×20),A5(20×25)。
选项A:(((A1×A2) ×A3) ×A4) ×A5,根据括号计算顺序,先计算A1×A2=A12(20×4),乘法次数为20×15×4=1200;然后计算A12×A3=A123(20×10),乘法次数为20×4×10=800;接着计算A123×A4=A1234(20×20),乘法次数为20×10×20=4000;最后计算A1234×A5=A12345(20×25),乘法次数为20×20×25=10000。
A选项乘法次数为1200+800+4000+10000=16000次;
选项A1×(A2×(A3×(A4×A5))) ,根据括号计算顺序,先计算A4×A5=A45(10×25),乘法次数为10×20×25=5000;然后计算A3×A45=A345(4×25),乘法次数为4×10×25=1000;接着计算A2×A345=A2345(15×25),乘法次数为15×4×25=1500;最后计算A1×A2345=A12345(20×25),乘法次数为20×15×25=7500。
B选项乘法次数为5000+1000+1500+7500=15000次;
C:((A1×A2)×A3)× (A4×A5) ,根据括号计算顺序,先计算A1×A2=A12(20×4),乘法次数为20×15×4=1200;然后计算A12×A3=A123(20×10),乘法次数为20×4×10=800;接着计算A4×A5=A45(10×25),乘法次数为10×20×25=5000;最后计算A123×A45=A12345(20×25),乘法次数为20×10×25=5000。
C选项乘法次数为1200+800+5000+5000=12000次;
选项D:(A1×A2) ×( (A3×A4)×A5) ,根据括号计算顺序,先计算A1×A2=A12(20×4),乘法次数为20×15×4=1200;然后计算A3×A4=A34(4×20),乘法次数为4×10×20=800;接着计算A34×A5=A345(4×25),乘法次数为4×20×25=2000;最后计算A12×A345=A12345(20×25),乘法次数为20×4×25=2000。
D选项乘法次数为1200+800+2000+2000=6000次;
D选项为最优计算顺序。