试题出自试卷《2013数学真题及解析》

问题1选项
A.条件（1）充分，但条件（2）不充分.
B.条件（2）充分，但条件（1）不充分.
C.条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分.
D.条件(1)充分，条件(2)也充分.
E.条件(1)和(2)单独都不充分，但条件(1)和条件(2)联合起来也不充分.

D

本题考查的是数列的周期性问题。先列举查找规律，再利用周期的求法解决问题。

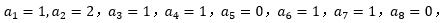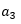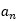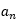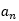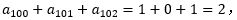条件一：k=2，则则从开始出现规律数1,1,0，即周期为3，则n-2若刚好被3整除，=0；若n-2被3整除余1，则=1；若n-2被3整除余2，则=1；因此充分。

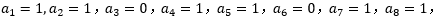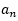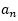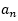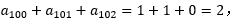条件二：k是小于20的正整数，假设k=1，则则从开始出现规律数1,1,0，即周期为3，则n若刚好被3整除，=0；若n被3整除余1，则=1；若n被3整除余2，则=1；因此成立。

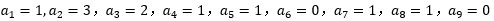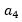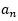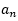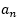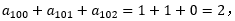假设k=3，则则从开始出现规律数1,1,0，即周期为3，则n-3若刚好被3整除，=0；若n-3被3整除余1，则=1；若n-3被3整除余2，则=1；因此成立。

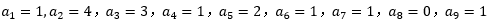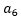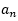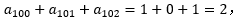假设k=4，则则从开始出现规律数1,1,0，即周期为3，则n-5若刚好被3整除，=0；若n-5被3整除余1，则=1；若n-5被3整除余2，则=1；因此成立。

假设k=19，则从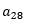开始出现规律数1,1,0，即周期为3，则n-27若刚好被3整除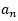，=0；若n-27被3整除余1，则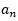=1；若n-27被3整除余2，则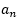=1；因此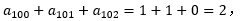成立。因而是充分。