试题出自试卷《【数学】管理类联考冲刺课3（课后练习）》

问题1选项
A.条件（1）充分，但条件（2）不充分.
B.条件（2）充分，但条件（1）不充分.
C.条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分.
D.条件(1)充分，条件(2)也充分.
E.条件(1)和(2)单独都不充分，但条件(1)和条件(2)联合起来也不充分.

D

答案：D
【考点判断】等差数列前n项和S_n最值问题

【解题必知】 确定等差数列前n项和S_n最值的方法

①单调性法：若已知a₁，则求S_n最值时，可利用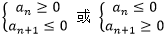确定

②函数法：若已知d，则可利用二次函数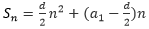求最值的求法

【解题思路】已知公差大于0，即数列单调递增，只需再确定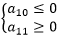，即可判断S_n在n=10处取最小值。

【解题步骤】
一、判断条件(1)，代入题干，即判断“已知{a_n}是公差大于零的等差数列，S_n是{a_n}的前n项和，且a₁₀=0，则S_n≥S₁₀”是否成立。

判断S_n≥S₁₀，即判断S_n在n=10处取是否最小值

已知公差大于0，则数列单调递增
又a_10=0，所以n<10时，a_n<0；n>10时，a_n>0

所以该等差数列满足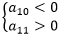，S_n在n=10处取最小值，则S_n≥S₁₀，条件充分。

二、判断条件(2)，代入题干，即判断“已知{a_n}是公差大于零的等差数列，S_n是{a_n}的前n项和，且a₁₁a₁₀<0，则S_n≥S₁₀”是否成立。

因为 a₁₁a₁₀<0 ，所以a₁₁ 、a₁₀为一正一负

又已知公差大于0，则数列单调递增，所以a₁₁ >a₁₀

于是可以判断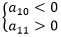：，S_n在n=10处取最小值，则S_n≥S₁₀，条件充分。选D。