试题出自试卷《管理类联考冲刺母题课后练习》

问题1选项
A.8
B.7
C.6
D.5
E.4

E

答案：E
【考点判断】最值函数
【解题必知】max表示取最大值
【解题思路】求出给出的函数的交点，在交点处分界，分别在每段中找出最大函数，最后连接每段找出的函数图像。
【解题步骤】

先计算出函数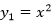与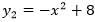的交点横坐标，再进行分段。

令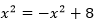，解得x=±2。

根据二次函数的图像性质可知，在(-∞,-2)时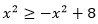，，此时f(x)=x²；

在[-2，2]时，-x²+8≥x²，此时f(x)=-x²+8；

在(2,+∞)时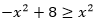，-x²+8≤x²，此时f(x)=x²

因此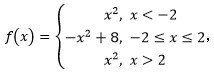

由此画出草图，可看出图像呈“W”型，因而在分界点取得最小值，即x=±2时，代入f(x)=x² 或-x²+8，得f(x)=4。