答案：D
【考点判断】 绝对值方程
【解题必知】
①绝对值的等价性：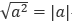
②完全平方公式：(a±b)2=a2+b2±2ab
【解题思路】多个绝对值的式子可移项再两边平方去绝对值，每次平方去掉一个绝对值。
【解题步骤】
方法一：因为|a+b|+|a-b|=6，由等价性得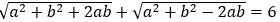
，
把ab=6代入式子得：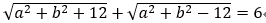
先移项得：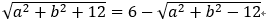
两边平方，整理得：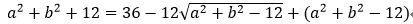
移项整理得：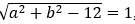
,
然后再两边平方得：a2+b2-12=1，解得：a2+b2=13。选D
方法二：特殊值法。已经a，b同号，根据已知条件假设a=3，b=2符合题意，因而 a2+b2=13 。
方法三：分析a和b的大小，①当a≥b时，因为|a+b|+|a-b|=6，得到a=3。由于ab=6，得到b=2，因此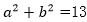 
。②当a<b时，同理，a+b+b-a=6，得到b=3。由于ab=6，得到a =2，因此 。
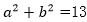