答案:A
【考点判断】等差数列的判断
【解题必知】
①数列的前n项和Sn与通项{an}的关系: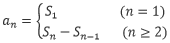
②判断等差数列的常用方法:
通项公式角度:观察数列通项是否满足an=dn+m这种形似关于 n 的一次函数形式
前n项和公式角度:观察数列前n项和是否满足Sn=An2+Bn这种形似关于 n 的一次函数形式(关键是不能含有常数项)
【解题思路】 根据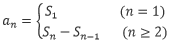 求出通项an的表达式,或者直接运用前n项和公式结论进行判断。
求出通项an的表达式,或者直接运用前n项和公式结论进行判断。
【解题步骤】
一、判断条件(1),代入题干,即判断“设数列{an}的前n项和为Sn,且Sn=n2+2n,则数列{an}是等差数列”是否成立。
当n=1时,a1=S1=3
当n≥2时, 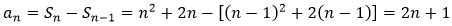
经验证当n=1,a1=3也符合该式
所以a_n=2n+1,该数列为等差数列,条件充分。
二、判断条件(2),代入题干,即判断“设数列 {an} 的前n项和为Sn,且Sn=n2+2n+1,则数列 {an} 是等差数列”是否成立。
当n=1时,a1=S1=4
当n≥2时, 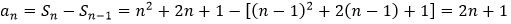
经验证当n=1,a1=4不符合该式,
所以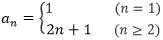 ,该数列不是等差数列,条件不充分。选A。
,该数列不是等差数列,条件不充分。选A。
方法二:
条件(1):Sn=n2+2n,满足等差数列Sn=An2+Bn形式,故该数列是等差数列。
条件(2):Sn=n2+2n+1含有常数项,不满足等差数列Sn=An2+Bn形式,故该数列不是等差数列。