试题出自试卷《几何冲刺课后练习》

问题1选项
A.条件（1）充分，但条件（2）不充分.
B.条件（2）充分，但条件（1）不充分.
C.条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分.
D.条件(1)充分，条件(2)也充分.
E.条件(1)和(2)单独都不充分，但条件(1)和条件(2)联合起来也不充分.

A

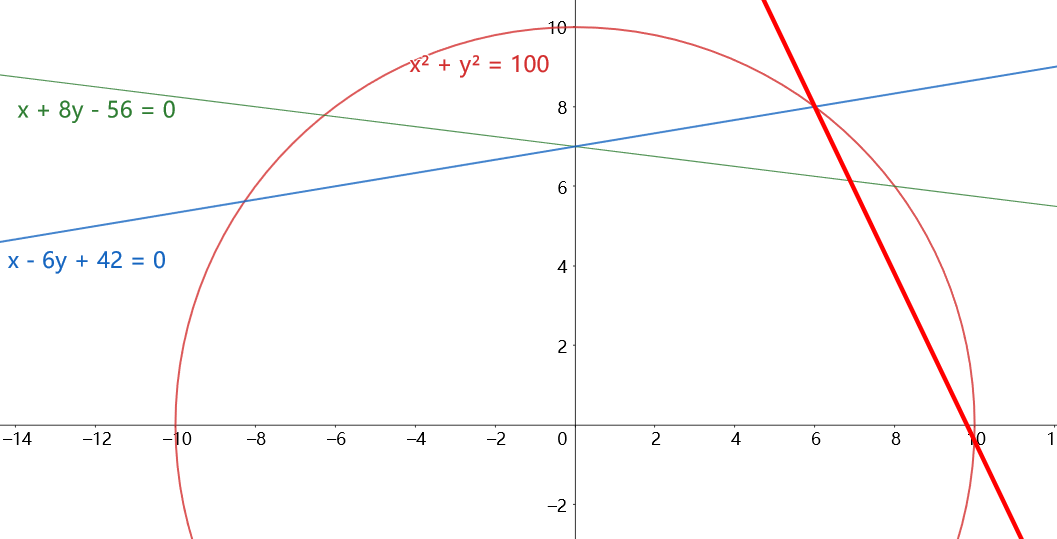
本题考查的是线性规划问题和不等式恒成立问题。解题思路就是将代数问题转化成几何图像问题，对任意的（x,y）∈D，lg⁡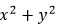()≤2，即 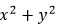≤100，这个可以看成以原点为圆心，半径为10，任意的点（x,y）∈D，都在圆内或圆上。设直线x+8y-56=0为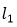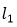，与圆的交点坐标为（8,6），设直线x-6y+42=0为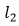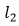，与圆的交点坐标为（6,8），且kx-y+8-6k=0(k<0)恒过定点（6,8），因此，当直线kx-y+8-6k=0(k<0)，过（6,8），（8,6）时为临界线，此时斜率k=-1。在黄线与蓝线之间都是可取范围，因而k≤-1是充分条件。为不满足条件。