阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。
【说明】
某工程计算中经常要完成多个矩阵相乘(链乘)的计算任务,对矩阵相乘进行以下说明。
(1)两个矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数,计算量主要由进行乘法运算的次数决定,假设采用标准的矩阵相乘算法,计算Amxn*Bnxp需要m*n*p次行乘法运算的次数决定、乘法运算,即时间复杂度为O(m*n*p)。
(2)矩阵相乘满足结合律,多个矩阵相乘时不同的计算顺序会产生不同的计算量。以矩阵A15×100,A2100*8,A38x50三个矩阵相乘为例,若按(A1*A2)*A3计算,则需要进行5*100*8+5*8*50=6000次乘法运算,若按A1*(A2*A3)计算,则需要进行100*8*50+5*100*50=65000次乘法运算。
矩阵链乘问题可描述为:给定n个矩阵,对较大的n,可能的计算顺序数量非常庞大,用蛮力法确定计算顺序是不实际的。经过对问题进行分析,发现矩阵链乘问题具有最优子结构,即若A1*A2**An的一个最优计算顺序从第k个矩阵处断开,即分为A1*A2*…*Ak和Ak+1*Ak+2*...*An两个子问题,则该最优解应该包含 A1*A2*…*Ak的一个最优计算顺序和 Ak+1*Ak+2*...*An 的一个最优计算顺序。据此构造递归式:
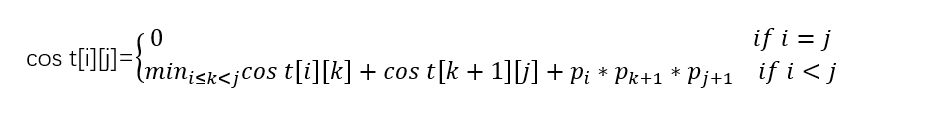
其中,cost[i][j]表示Ai+1*Ai+2*...Aj+1的最优计算的计算代价。最终需要求解cost[0][n-1]。
【C代码】
算法实现采用自底向上的计算过程。首先计算两个矩阵相乘的计算量,然后依次计算3个矩阵、4个矩阵、…、n个矩阵相乘的最小计算量及最优计算顺序。下面是该算法的语言实现。
(1) 主要变量说明
n:矩阵数
seq[]:矩阵维数序列
cost[i][j]:二维数组,长度为n*n,其中元素cost[i][j]表示Ai+1*Ai+2**Aj+1的最优的计算代价。
trace[][]:二维数组,长度为n*n,其中元素trace[i][j]表示Ai+1*Ai+2**Aj+1的最优计算顺序对应的划分位置,即k。
(2)函数cmm
#define N100
int cost[N[N];
int trace[N][N];
int cmm(int n,int seq[]){
int tempCost;
int tempTrace;
int i,j,k,p;
int temp;
for(i=0; i<n-p;i++){
(1) ;
tempCost = -1;
for(k = i; (2) ;k++){
temp= (3) ;
if(tempCost==-1 || tempCost>temp){
tempCost = temp;
tempTrace=k;
}
}
cost[i][j] = tempCost;
}
}
return cost[0][n-1];
}
【问题1】(8分)
根据以上说明和C代码,填充C代码中的空(1)~(4)。
【问题2】(4分)
根据以上说明和C代码,该问题采用了(5)算法设计策略,时间复杂度为(6)(用O符号表示)。
【问题3】(3分)
考虑实例n=4,各个矩阵的维数为A1为15*5,A2为5*10,A3为10*20,A4为20*25,即维度序列为15,5,10,20和25。则根据上述C代码得到的一个最优计算顺序为(7)(用加括号方式表示计算顺序),所需要的乘法运算次数为 (8)。