试题出自试卷《一元二次方程02课后练习》

问题1选项
A.条件(1)充分，但条件(2)不充分。
B.条件(2)充分，但条件(1)不充分。
C.条件(1)和条件(2)单独都不充分，但条件(1)和条件(2)联合起来充分。
D.条件(1)充分，条件(2)也充分。
E.条件(1)和条件(2)单独都不充分，条件(1)和条件(2)联合起来也不充分。

D

答案：D
【考点判断】韦达定理的变形
【解题必知】
①韦达定理：一元二次方程ax²+bx+c=0(a≠0)的两个根分别是x₁，x₂

则有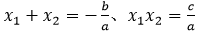：(注意：运用韦达定理的前提是∆≥0)

②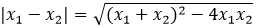或者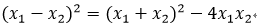 

【解题思路】根据底数的范围确定对数函数的单调性，根据单调性比较对数值的大小。
【解题步骤】
一、判断条件(1)，代入题干，即判断“方程2x²-ax-x+a+3=0的两实根为x₁ 、x₂，且a=-3，则|x₁-x₂ |=1”是否成立。

方程化成标准形式：2x²-(a+1)x+a+3=0

由韦达定理得：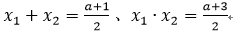

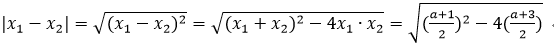
把a=-3代入，得|x₁-x₂|=1，条件充分。

二、判断条件(2)，代入题干，即判断“方程2x²-ax-x+a+3=0的两实根为x₁、x₂，且a=9，则|x₁-x₂|=1”是否成立。

把a=9代入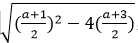，得|x₁-x₂ |=1，条件充分。选D。