【考点】本题考查多元函数积分学及其应用-二重积分-二重积分的概念与性质-二重积分的概念及性质
【解题思路】由题意知，积分区域为{(x,y)|0≤x≤1,x≤y≤1}，也可表示为{(x,y)|0≤y≤1,0≤x≤y}，故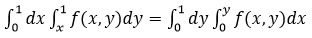
．
【希赛点拨】
二重积分的定义
设z=f(x,y)是定义在有界闭区域D上的有界函数，将区域D任意分割成n个无公共内点的小区域Di (i=1,2,⋯,n)，其相应的面积记为∆σi，对任意一点(xi,yi)∈Di(i=1,2,⋯,n)，作和式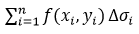
，以d(Di)表示小区域Di的直径，记
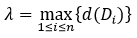，如果λ→0时
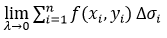总存在，且与闭区域D的分法及点(xi,yi)的取法无关，则称二元函数f(x,y)在区域D上是可积的，并称此极限为函数f(x,y)在区域D上的二重积分，记作
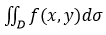，即
．
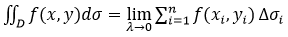其中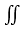
称为二重积分号，D称为积分区域，f(x,y)称为被积函数，dσ称为面积元素，x，y称为积分变量，
称为（二重）积分和．
=_________．
