本题考查 数学与经济管理 的基础知识。
这里其实就是在矩阵中找出四个元素,分别位于不同行,不同列,使其和达到最大值,从而求解出总效益最大的方案。这里转换为求总和最小的方案个数更方便求解。用 矩阵中的最大元素 6减去每个数得到的非负整数新矩阵,如下:
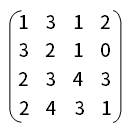
根据矩阵的特性:任一行(或列)各元素都减(或加)一常数后,并不会影响最优方案的位置,只是目标值(分配方案的各项总和)也减(或加)了这一常数。
这里可以利用特性使矩阵更多的元素变成0,以利于直观求解。
第一列减去最小数1,第二列减去最小数2,第三列减去最小数1,第四列最小数已经为0了,所以不变,变换后矩阵如下:
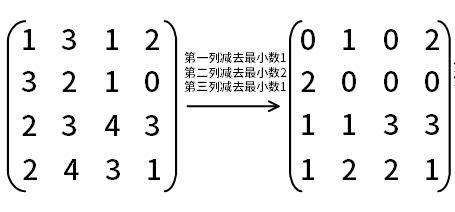
然后继续第三行减去最小数1,第四行减去最小数1,第一行和第二行最小数已经为0了,所以不变,变换后矩阵如下:
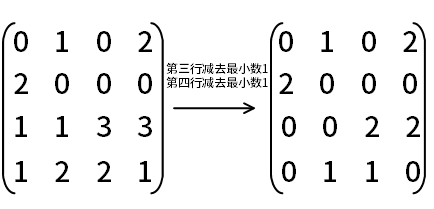
从第1列看,若取(1,1)的0,则其余三个0元素肯定位于(4,4)、(3,2)、 (2,3);
若取(3,1)的0,则其余三个0元素肯定位于(1,3)、(4,4)、 (2,2);
若取(4,1)的0,则其余三个0元素肯定位于(1,3)、(3,2)、 (2,4)。
因此,最优方案共有三个,每小时的总效益都是18,答案选择C选项。
①分配甲-A,乙-C, 丙-B,丁-D;
②分配甲-C,乙-B, 丙-A,丁-D;
③分配甲-C,乙-D,丙-B,丁-A。