【考点判断】应用题—行程问题
【解题思路】行船问题模型
【解题步骤】
设水速为v水,船速为v船,起航后t分钟木板落水(如下图所示).
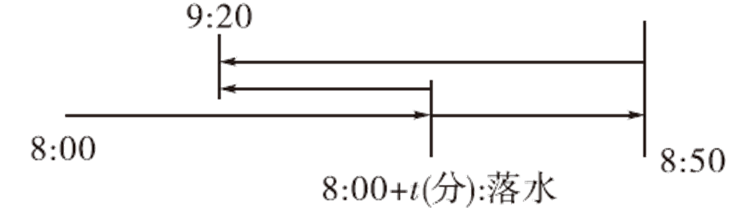
从木板落水到船员发现,用时(50−t)分钟
此时木板顺水走了(50−t)⋅v水,船逆水走了(50−t)(v船−v水 ),
从8:50发现木板丢失到9:20追上,共用30分钟,追及距离为
(50−t)⋅v水+(50−t)(v船−v水),
则有等式[(v船+v水)−v水]×30=(50−t)⋅v水+(50−t)(v船−v水 ),
解得:t=20,即8:20木板落水.
快速得分技巧:(极限分析法)假设水速为零,则木板落入水后静止不动,从8:50发现木板丢失到9:20追上木板耗时30分钟,说明木板为8:50之前30分钟丢失,即8:20.
故选D.