试题出自试卷《几何冲刺课后练习》

问题1选项
A.[2,18]
B.[2,20]
C.[2,36]
D.[4,18]
E.[4,20]

B

本题考查的是绝对值不等式与解析几何的实际意义。本题可以采用技巧法，即特殊值验证法。还可采用基础解法，即利用三角不等式。已知|x-2|+|y-2|≤2，由三角不等式可知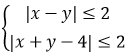，根据数形结合，画出区域，即一个平行四边形区域。再因为x^2+y^2表示的是区域内的点与原点距离的平方，可知距离最小值为原点向区域做垂线段时取得，距离最大值为最远边界点与原点连线取得。因此可知在（1,1）处取得最小值，在（2,4）或（4,2）处取得最大值。因此代入可知x²+y²的取值范围是[2,20] 。