2019年高考高起点数学(文史财经类)押题卷三

2019年高考高起点数学(文史财经类)押题卷三，本试卷是2019年高考数学(文)的全真模拟试题。

一、单项选择题

1.若集合，则S∪T是（）。

A.

2.设x ，y为实数，则I x | = | y |成立的充分必要条件是（）。

A.
B.
C.
D.

3.函数的图像之间的关系是（）。

A.关于原点对称
B.关于x轴对称
C.关于直线y = 1对称
D.关于y轴对称?

4.随机抽取10名小学生，他们出生在不同月份的概率为（　　）

A.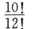
B.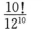
C.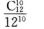
D.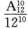

5.已知向量a=（2，-4），b=（1，2），c=（1，-2），d=（-2，-4），则其中共线的有（　　）

A.a与d共线，b与c共线
B.a与b共线，c与d共线
C.a与c共线，b与d共线
D.以上答案都不正确

6.设成等比数列，则x等于（）。

A.1 或-2
B.1 或-1
C.0 或-2
D.- 2

7.已知直线y=3x + 1与直线x+ my + 1 = 0互相垂直，则m的值是（）。

A.1/3
B.-1/3
C.-3
D.3

8.椭圆的长轴是短轴的二倍，则椭圆的离心率是（）。

A.
B.
C.
D.

9.函数，当x∈[-2，+∞)时是增函数，当x∈(-∞，-2]时是减函数，则f(1)= （）。

A.-3
B.13
C.7
D.由m而定的常数

10.抛物线=－4x上一点P到焦点的距离为4，则它的横坐标是（　　）

A.－4
B.－3
C.－2
D.－1

11.双曲线的中心在原点且两条渐近线互相垂直，且双曲线过(-2，0)点，则双曲线方程是（）。

A.
B.
C.
D.

12.若，则f (x + 2)= （）。 

A.
B.
C.
D.

13.已知M（3，－1），N（－3，5），则线段MN的垂直平分线方程为（　　）。

A.x－y－2=0
B.x+y－2=0
C.3x－2y+3=0
D.x－y+2=0

14.不等式的解集是实数集，则m的取值范围是（）。

A.m＜16/9
B.m＞0
C.0＜m＜16
D.0≤m≤16/9

15.同时抛掷两颗正六面体的骰子，则出现点数之和等于6的概率为（）。

A.1/11
B.5/11
C.5/36
D.10/132

16.曲线在点(0，c)处的切线的倾斜角为（）。

A.π/2
B.π/3
C.π/4
D.π/6

17.已知数列前n项和，则第5项的值是（）。

A.7
B.10
C.13
D.16

二、填空题

1.某灯泡厂生产25 w电灯泡，随机地抽取7个进行寿命检查（单位：h），结果如下：1487，1394，1507，1528，1409，1587，1500，该产品的平均寿命估计是________，该产品的寿命方差是________．

2.不等式|6x-1/2|≥3/2的解集是_____。

3.函数的定义域为______.

4.从5位男生和4位女生中选出2人作代表，恰好一男生和一女生的概率是______.

三、解答题

1.(Ⅰ)求f(x)的图象在x=3处的切线方程；(Ⅱ)求f(x)在 区间[0，4]上的最大值和最小值

2.已知二次函数图像过点P(1，0)，并且对于任意实数x，有f(1+x)=f (1- x)，求函数f(x)的最值。

3.记等比数列{an}的前n项和为Sn，已知S3+S6=2S9，求该等比数列的公比q．

4.(Ⅰ)求m的值；(Ⅱ)如果P是两曲线的一个公共点，且F1是椭圆的另一焦点，求△PF1F2的面积．