山东省专升本考试（土木工程）综合一模拟试卷4

山东省专升本考试（土木工程）综合一模拟试卷4,本试卷总分60分，共有2类型题目。

一、1. 高等数学

高等数学 总分为：50

1.设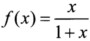
，则f[f(x)]=( )。

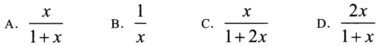
A． 
B． 
C． 
D． 

2.当x→1时，与2sin²(x—1)等价的无穷小量为( )。

A．2(x—1)
B．(x—1)²
C．2ln(2x—1)
D．2e(x—1)²—2

3.已知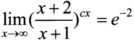
，则常数C的值为( )。

A．—1
B．—2
C．1
D．2

4.不定积分ftan xdx=( )。

A．ln｜sinx｜+C
B．-ln｜cosx｜+C
C．-ln｜sinx｜+C
D．-ln｜cosx｜+C

5.微分方程dy=2xy的通解为( )。

A．y=e^x+C
B．y=Ce^x2
C．y=e^x2+C
D．y=x²+C

6.x²+y²=1在空间表示_________曲面．

7.已知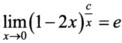
，则常数C=_________．

8.曲线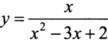
的水平渐近线为_________．

9.已知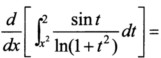
_________．

10.若a＞0，b＞0均为常数，则极限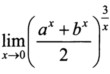
=_________．

11.设x∈[-1，1]，则arcsinx+arccosx=_________．

12.过点(-3，0，2)且垂直于平面3x—2y+z=1的直线方程为_________．

13.设函数z=e^xy，则dz｜_(e，1)=_________．

14.幂级数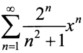
的收敛区间为__________．

15.微分方程y+2y+5y=0的通解为__________．

16.

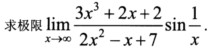
17.

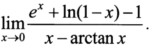
18.设函数z=x^sinyy，求dz．

19.求不定积分∫x²lnxdx．

20.设函数z=z(x，y)由方程sin(x²y)+e^xyz—xy²=0所确定，求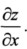

21.求微分方程y—2y+y=xe^x的通解．

22.求二重积分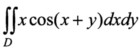
，其中D是以(0，0)，(π，0)，(π，π)为顶点的三角形闭区域．

23.求幂级数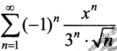
的收敛半径和收敛域．

24.已知f(x)在(-∞，+∞)内可导，且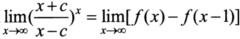
，C为常数，又知
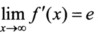，试证：C=1/2． (提示：使用微分中值定理)

二、2. 混凝土结构

混凝土结构 总分为：50

1.简述大、小偏心受压构件的产生条件和破坏特征。

2.什么是先张法? 简述先张法预应力混凝土施工步骤及主要设备。

3.已知某柱子设计使用年限为50年，截面尺寸b×h=400mm×600mm，a_s=a_s=45mm， 混凝土用C25，f_c=11．9N／mm²，受压一侧钢筋4φ22，(A_s=1520mm²，f_y=f_y=300N／mm²，ζ_B=0．55)，受拉一侧钢筋2φ20，(A_s=628mm²，f_y=f_y=300N／mm²，柱子计算长度ι₀5．5m,偏心距e₀=350mm，求构件截面的承载力设计值N和弯矩设计值M。