山东省专升本综合一（机械设计制造及其自动化）模拟试卷7

山东省专升本综合一（机械设计制造及其自动化）模拟试卷7,本试卷总分100分，共有2类型题目。

一、1. 高等数学

高等数学 总分为：50

1.f(x)在[a，b]上连续是f(x)在[a，b]上有界的( )条件。

A．充分
B．必要
C．充要
D．非充分也非必要

2.当x→0⁺时，( )与x是等价无穷小量。

A．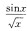
B．1n(1+x)
C．x²(x+1)
D．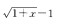

3.f(x)在x=0的某邻域内一阶导数连续且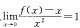
则( )。

A．x=0不是f(x)的极值点
B．x=0是f(x)的极大值点
C．x=0是f(x)的极小值点
D．x=0是f(x)的拐点

4.设f(x)在x=a某邻域内连续且f(a)为极大值，则存在δ>0，当x∈(a一δ，a+δ)时，必有( )。

A．(x—a)[f(x)一f(a)]≥0
B．(x—a)[f(x)一f(a)]≤0
C．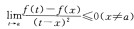
D．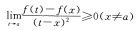

5.设f(x)，g(x)在[a，b]上连续，则( )。

A．若,则在[a，b]上f(x)=0
B．若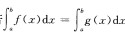，则在[a，b]上f(x)=g(x)
C．若a
D．若f(x)≤g(z)，则

6.
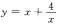的极大值是_________；极小值是________。

7.
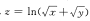，求xz_x+yz_y=_____________。

8.设函数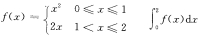
=___________。

9.∫f(x)dx=F(x)+则∫c^-xf(e^-x)dx=__________。

10.若函数f(x)的导函数为sinx，则f(x)的一个原函数是__________。

11.

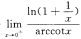
12.
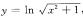求y(2)。

13.
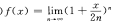求df(x)。

14.

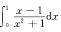
15.x=f(x，y)由x²+y²+z²=1确定，求z_x，z_y。

16.求函数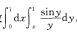

17.求函数I(x)=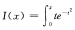
的极值。

二、2. 工程力学

工程力学 总分为：50

1.下列关于构件的几何形状说法不正确的是( )。

A．轴线为直线的杆称为直杆
B．轴线为曲线的杆称为曲杆
C．等截面的直杆简称为直杆
D．横截面大小不等的杆称为截面杆

2.内力和应力的关系式( )。

A．内力小于应力
B．内力等于应力的代数和
C．内力为矢量，应力为标量
D．应力是分布内力的集度

3.为了提高混凝土的抗拉强度，可在梁中配置钢筋。若矩形截面梁的弯矩图如图所示，梁中钢筋(图中虚线所示)配置最为合理的是( )。

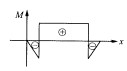
A．
B．
C．
D．

4.质量m=10kg的物体M，放在倾角a=30^。的斜面上，用刚度系数k=100N／m的弹簧系住，如图所示。斜面与物体的动摩擦因数f=0．2，当物体由弹簧原长位置M₀沿斜面运动到M₁时，作用于物体上的各力在路程s=0．5m上做的功计算不准确的是( )。

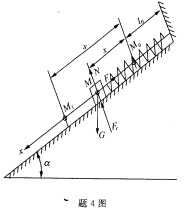
A．W_G=24．5J
B．W_N=0
C．W_F^"=8．5J
D．W_F=12．5J

5.一端固定，一端为弹性支撑的压杆，如图所示，其长度系数的范围为( )。

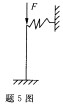
A．μ<0．7
B．μ>2
C．0．7<μ<2
D．不能确定

6.滑轮半径r=0．2m，可绕水平轴O转动，轮缘上缠有不可伸长的细绳，绳的一端挂有物体A，如图所示。已知滑轮绕轴0的转动规律φ=0．15t³rad，其中t单位为s，当t=2s时，轮缘上M点的速度、加速度和物体A的速度、加速度计算不正确的是( )。

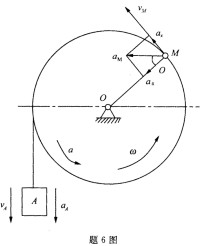
A．M点的速度为v_M=0．36m／s
B．M点的加速度为a_M=0．648m／s²
C．物体A的速度为v_A=0．36m／s
D．物体A的加速度为a_A=0．36m／s²

7.如图所示，在半径为R的铁环上套一小环M，杆AB穿过小环M并匀速绕A点转动，已知转角φ=ωt(其中ω为一常数，φ的单位为rad，t的单位为s)，开始时AB杆处于水平位置，则当小环M运动到图示位置时(以MO为坐标原点，小环Md运动方程为正方向建立自然坐标轴)，下面说法不正确的一项是( )。

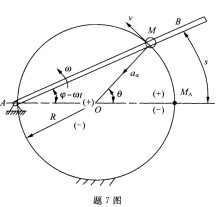
A．小环M的运动方程为s=2Rωt
B．小环M的速度为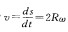
C．小环M的切向加速度为0
D．小环M的法向加速度为2Rω²

8.工程区分塑性材料和脆性材料的标准是看其延伸率艿大小等于还是大于( )。

A．1％
B．3％
C．5％
D．10％

9.用积分法求一悬臂梁受力后的变形时，边界条件为：在梁的固定端处( )。

A．挠度为零，转角也为零
B．挠度为零，转角不为零
C．挠度不为零，转角为零
D．挠度不为零，转角也不为零

10.两简支梁，一根为钢，一根为铜。已知它们的跨度和抗弯刚度均相同，若在跨中有相同的载荷F，二者的关系是( )。

A．支反力不同
B．最大正应力不同
C．最大挠度不同
D．最大转角不同

11.关于静滑动摩擦，下面说法中不正确的是( )。

A．可由平衡条件确定
B．0≤F_f≤F_∫max
C．F_∫max=f_sF_N
D．F_f=F_B+F_N

12.在图示平面刚架上，m－m截面上的内力分量不为零的是( )。

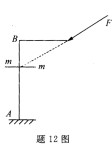
A．F_N、F_s、M
B．F_N、F_s
C．M、F_N
D．M、F_s

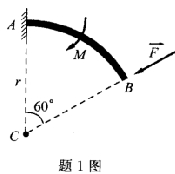
13.半径为r的圆弧形杆AB(C为其圆心)的一端A固定于墙上，杆在已知力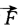
和力偶矩为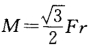
的力偶作用下平衡，若不计杆的自重，试求固定端A处的约束反力。

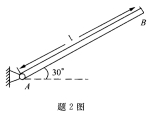
14.均质细长直杆AB的质量为m，长度为l，可在铅垂面内绕A轴转动。若在图示杆与水平线夹角30^。处将杆无初速释放，不计轴承处摩擦，试求该瞬时固定铰链支座A处的约束反力。

15.一直径d=16mm、长l=3m的圆截面直杆，在轴向拉力F=30kN作用下，伸长出△l=2．2mm，试求杆材料的弹性模量E。

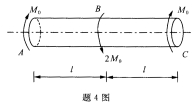
16.图示受扭圆轴，已知截面的极惯性矩I_p和材料的切变模量G。试求A、C两截面间的相对扭转角φ_AC。