山东省专升本考试土木工程结构力学（力 法）模拟试卷1

山东省专升本考试土木工程结构力学（力 法）模拟试卷1,本试卷总分39分，共有1类型题目。

一、2. 结构力学

结构力学 总分为：50

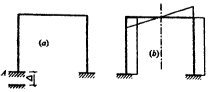
1.下图(a)所示对称结构在支座移动下的弯矩图形状如下图(b)所示。 ( )

A．正确
B．错误

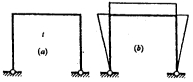
2.下图(a)所示对称结构，内部温度升高t，其弯矩图形状如下图(b)所示。 ( )

A．正确
B．错误

3.在下图中由于弯矩图不满足。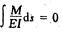，所以它是错误的。 ( )

A．正确
B．错误

4.在力法计算时，多余未知力由位移条件来求，其他未知力由平衡条件来求。( )

A．正确
B．错误

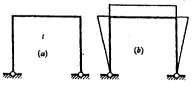
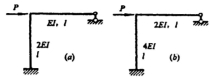
5.在下图所示结构中若增大柱子的EI值，则梁跨中点截面弯矩值减少。 ( )

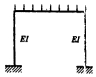
A．正确
B．错误

6.对下图(a)所示结构，选(b)为基本体系，则力法典型方程为δ₁₁X₁+△_1P=0。 ( )

A．正确
B．错误

7.下图(a)和下图(b)为同一结构的两种外因状态，若都选下图(c)为基本体系计算，则它们的力法方程中的主系数相同，副系数相同，自由项不同，右端项不同。( )

A．正确
B．错误

8.在下图所示结构中，如将刚节点A化成铰节点，相当于去掉了两个约束。 ( )

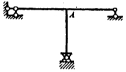
A．正确
B．错误

9.在图所示一次超静定结构中，不能作为力法基本未知量的是 ( ) 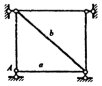①任一竖向支杆的反力；②任一水平支杆的反力；④a杆轴力；④b轩轴力

A．1、2、3、4
B．1、3,4
C．1、2
D．2、3

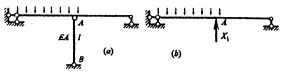
10.在图所示结构中，若增大拉杆的刚度EA，则梁内D截面弯矩如何? ( )

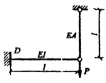
A．不变
B．增大
C．减小
D．可能会下侧受拉

11.在图所示结构中，若减小拉杆的刚度EA，则梁内D截面弯矩如何?( )

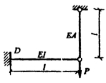
A．不变
B．增大
C．减小
D．可能会大于pl

12.图(a)结构如选图(b)为基本体系，其力法方程为( )

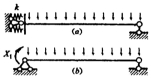
A．δ₁₁X₁+△_1P=0
B．δ₁₁X₁+△_1P=l／k
C．δ₁₁X₁+△_1P=-X₁／k
D．δ₁₁X₁+△_1P=X₁+k

13.图所示结构各杆E=常数，在给定荷载作用下，若使A支座反力为零，则应使( )

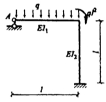
A．I₁=I₂
B．I₁=2I₂
C．I₁=4I₂
D．4I₁=I₂

14.图所示结构各杆EI=常数，在给定荷载作用下，若使A支座反力为零。则应使( )

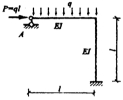
A．P=ql
B．P=0．5ql
C．P=I．5ql
D．P=1．25ql

15.图所示十字架超静定刚架，各杆EI相同，在图示荷载作用下，Q_AB为( )

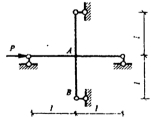
A．0．5P
B．0．25P
C． 一0．25P
D．0

16.图所示两结构跨中点截面的弯矩之间的关系是 ( )

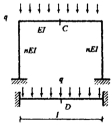
A．跨中点截面的弯矩相等
B．C截面弯矩大于D截面弯矩
C．当n很大时C截面弯矩小于D截面弯矩
D．当n很小时C截面弯矩小于D截面弯矩

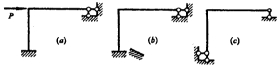
17.图所示各结构在图示荷载作用下，产生弯矩的是 ( )

A． 
B． 
C． 
D． 

18.图(a)所示结构，取图(b)所示基本体系计算，下列结论正确的是( )

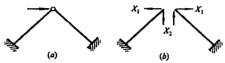
A．结构弯矩、剪力为零
B．结构轴力为零
C．X₁=0
D．X₂=0

19.下列关于图所示两结构论述错误的是 ( )

A．内力相同
B．反力相同
C．应力相同
D．结构(a)的变形大

20.下列哪个结构的半边结构不是图(a)所示结构? ( )

A． 
B． 
C． 
D． 

21.下列哪个结构的半边结构不是图(a)所示结构? ( )

A． 
B． 
C． 
D． 

22.图(a)梁因温度变化引起的弯矩如图(b)，线膨胀系数为口，梁截面(矩形)高度为h，右端转角(顺时针为正)为 ( )

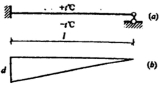
A．0
B．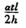
C．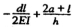
D．B和C都是正确答案

23.试用力法解下图所示连续梁，并画弯矩图。(EI=常数)

24.试用力法解下图所示刚架，并画弯矩图。(EI=常数)

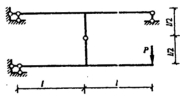
25.用力法求下图所示结构的内力，并讨论：当刚度比k=EI／EA变化时，各杆内力的变化规律及由此应得出的结论。

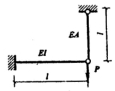
26.试用力法懈下图所示刚架，并画弯矩图。(EI=常数)

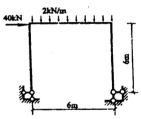
27.对下图(a)结构，按下图(b)所给的基本体系进行计算，并绘制弯矩图。

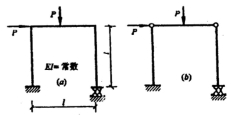
28.对下图(a)结构，按下图(b)所给的基本体系进行计算绘制弯矩图，并解释力法方程的物理意义。

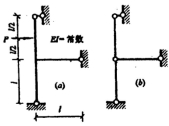
29.试用力法作下图所示对称刚架弯矩图，并求横梁中点挠度。(EI=常数)

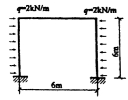
30.下图所示框架各杆截面EI相同，如果四角点的弯矩为零，则P₁和P₂的比值应为多少?

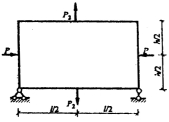
31.下图所示简支梁E=20GPa，矩形截面b×h=20cm×50cm，在梁的中点处距离梁底1cm有一刚性楔块，在下图示荷载作用下，C点与刚性块接触，用力法计算，作弯矩图。

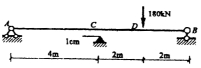
32.求下图所示超静定梁，由于C支座移动所引起的B截面的转动。

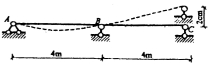
33.试用力法计算下图所示结构作弯矩图，并校核。各杆EI为常数，k₁=12EI／l，k₂=EI／l³。

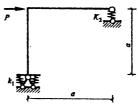
34.试用力法计算下图所示结构，并作弯矩图。各杆EI为常数，k=3EI／l³。

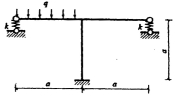
35.试用力法计算下图所示结构，并作弯矩图。各杆EI，a为常数。h=0．1a。

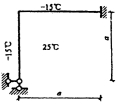
36.下图(a)所示变截面梁，用力法计算并取下图(b)所示的基本体系，则可列出力法方程δ₁₁X₂+△_Q=△₁，试写出δ₁₁、△_Q、△₁的具体表达式。

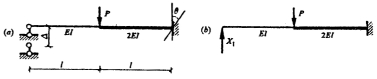
37.计算下图所示等截面梁，并画弯矩图。

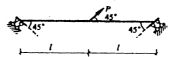
38.已知下图(a)所示结构角点处截面弯矩为Pa／8(外侧受拉)，利用这一结论，计算下图(b)所示结构，并作弯矩图。