山东省专升本考试土木工程结构力学（结构动力计算）模拟试卷2

山东省专升本考试土木工程结构力学（结构动力计算）模拟试卷2,本试卷总分40分，共有1类型题目。

一、2. 结构力学

结构力学 总分为：50

1.一般情况下，振动体系的自由度与超静定次数无关。 ( )

A．正确
B．错误

2.具有集中质量的体系，其动力计算自由度就等于其集中质量数。 ( )

A．正确
B．错误

3.下图所示体系有3个振动自由度。 ( )

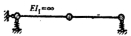
A．正确
B．错误

4.下图所示体系有一个振动自由度。 ( )

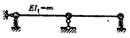
A．正确
B．错误

5.由于体系的自由度与超静定次数无关，所以所示两体系振动自由度相同。 ( )

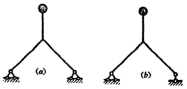
A．正确
B．错误

6.结构的自振频率与质量、刚度及荷载有关。 ( )

A．正确
B．错误

7.自由振动过程中无外荷载作用。 ( )

A．正确
B．错误

8.无阻尼单自由度体系在简谐荷载作用下，当k₁₁＞mθ²，荷载与位移同向。 ( )

A．正确
B．错误

9.无阻尼单自由度体系在简谐荷载作用下，当mδ₁₁θ²，荷载与位移反向。( )

A．正确
B．错误

10.无阻尼单自由度体系在简谐荷载作用下，β随θ／ω的增大而增大。 ( )

A．正确
B．错误

11.动力系数β也称为动力放大系数，它总是大于l的。 ( )

A．正确
B．错误

12.结构动力计算的基本未知量是 ( )

A．质点位移
B．节点位移
C．多余未知力
D．杆端弯矩

13.无阻尼单自由度体系的自由振动方程：y(t)=C₁sinωt+C₁cosωt。则质点的振幅y_max。 ( )

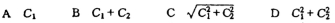
A． 
B． 
C． 
D． 

14.下图所示四结构，柱子的刚度、高度相同，横梁刚度为无穷大，质量集中在横梁上。它们的自振频率自左至右分别为ω₁、ω₂、ω₃、ω₄，那么它们的关系是 ( )

A． ω₁=ω₂＜ω₃＜ω₄
B． ω₁＜ω₂＜ω₃＜ω₄
C．ω₁=ω₂=ω₃=ω₄
D．ω₁＜ω₂=ω₃＜ω₄

15.下图所示四结构，柱子的刚度、高度相同，横梁刚度为无穷大，质量集中在横梁上。它们的自振频率自左至右分别为ω₁、ω₂、ω₃、ω₄，那么它们的关系是 ( )

A． ω₁=ω₂＜ω₃＜ω₄
B． ω₁＜ω₂＜ω₃＜ω₄
C．ω₁=ω₂=ω₃=ω₄
D．ω₁＜ω₂=ω₃＜ω₄

16.不计阻尼，不计自重，不考虑杆件的轴向变形，下图所示体系的自振频率为( )

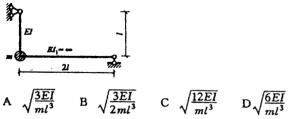
A． 
B． 
C． 
D． 

17.下图所示四个相同的桁架，只是集中质量m的位置不同，它们的自振频率分别为ω_a、ω_b、ω_c、ω_d(忽略阻尼及竖向振动作用，各杆EA为常数)，那么它们的关系是 ( )

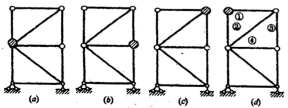
A．ω_a=ω_b＜ω_c=ω_d
B．ω_a＜ω_b＜ω_c＜ω_d
C．ω_a=ω_b＞ω_c=ω_d
D．ω_a＞ω_b＞ω_c＞ω_d

18.设ω为结构的自振频率，θ为荷载频率，β为动力系数下列论述正确的是( )

A．ω越大β也越大
B．θ越大β也越大
C．θ／ω越大β也越大
D．θ／ω越接近1，β绝对值越大

19.当简谐荷载作用于有阻尼的单自由度体系质点上时，若荷载频率远远大于体系的自振频率时，则此时与动荷载相平衡的主要是 ( )

A．弹性恢复力
B．阻尼力
C．惯性力
D．重力

20.无阻尼单自由度体系在简谐荷载作用下，共振时与动荷载相平衡的是 ( )

A．弹性恢复力
B．惯性力
C．惯性力与弹性力的合力
D．没有力

21.如果体系的阻尼数值增大，下列论述错误的是 ( )

A．自由振动的振幅衰减速度加快
B．自振周期减小
C．动力系数减小
D．位移和简谐荷载的相位差变大

22.下图(a)、(b)两体系中，EI、m相同，则两者自振频率的关系是 ( )

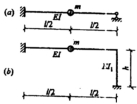
A．ω_a＞ω_b
B． 当EI₁》EI时ω_a≈ω_b
C．ω_a=ω_b
D．当EI₁《EI时ω_a≈ω_b

23.下图所示3个单跨梁的自振频率分别为ω_a、ω_b、ω_c它们之间的关系是( )。

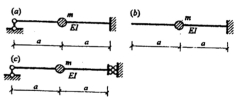
A．ω_a＞ω_b＞ω_c
B．ω_a＞ω_c＞ω_b
C．ω_c＞ω_a＞ω_b
D．ω_b＞ω_a＞ω_c

24.一单自由度振动体系，由初始位移0．685cm，初始速度为零产生自由振动，振动一个周期后最大位移为0．50cm，体系的阻尼比为 ( )

A．ζ=0．05
B．ζ=0．10
C．ζ=0．15
D．ζ=0．20

25.一单自由度振动体系，其阻尼比为ζ，共振时的动力系数为β则 ( )

A．ζ=0．05，β=10
B．ζ=0．10，β=15
C．ζ=0．15，β=20
D．ζ=0．20，β=25

26.下图所示体系频率比为θ／ω，动位移y(t)与荷载P(t)的关系是 ( )

A． 当θ／ω＞1对，y(t)与P(t)同向，当θ／ω＜1时，y(t)与P(t)反向
B． 当θ／ω＞l时，y(t)与P(t)反向，当θ／ω＜1时，y(t)与P(t)同向
C．不论θ／ω如何，y(t)与P(t)同向
D．不论θ／ω如何，y(t)与P(t)反向

27.下图所示体系，当荷载频率θ接近结构的自振频率ω时 ( )

A．可作为静荷载处理
B．可以不考虑阻尼对频率的影响
C．荷载影响非常小
D．可以不考虑阻尼对振幅的影响

28.已知结构的自振周期T=0．3s，阻尼比ξ=0．1，质量m，在y₂=3mm，V₀=0的初始条件下开始振动，则经过几个周期后振福可以衰减到0．Imm以下? ( )

A．3
B．4
C．5
D．6

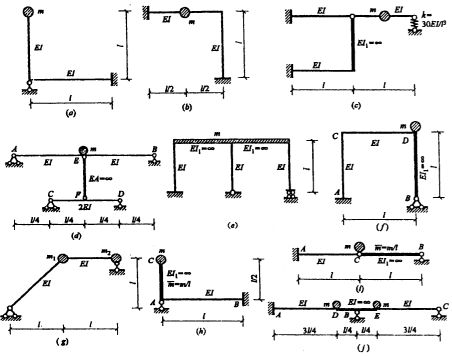
29.求下图所示体系的自振频率。除特殊标注外，其余各杆不计质量。

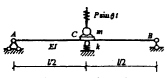
30.下图所示梁中点电机的质量为m，不计梁的自重和阻尼，求动位移幅值和动弯矩幅值。其中弹簧刚度系数k=12EI／l³，荷载频率θ²=36EI／(ml³)。

31.下图所示简支梁，若不计梁的自重和阻尼，求当θ₁=0．8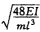，θ₂=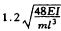时，质点的动位移幅值和动弯矩幅值下图。

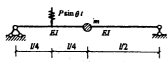
32.下图所示结构，质量集中在横梁上，不计阻尼，求当θ=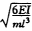时动弯矩幅值下图。

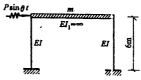
33.下图所示结构，不计阻尼，θ=0．5ω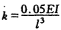，，求频率和质点振幅。

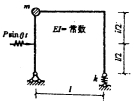
34.下图所示刚架不计自重和阻尼，求当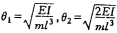时，质点的动位移幅值和A截面动弯矩幅值。

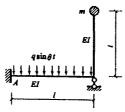
35.求下图所示体系频率和主振型，并演算主振型正交性。