2015年成人高考高升本《数学理工类》冲刺试卷(4)
摘要:2015年成人高考高升本《数学理工类》冲刺试卷(4),本试卷总分150分,共有3类型题目。
2015年成人高考高升本《数学理工类》冲刺试卷(4),本试卷总分150分,共有3类型题目。
一、选择题:每小题5分,共85分,在每小题给出的四个选项中,只有一项是符合题目要求。
1.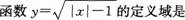 ( )
( )
A.{x|x≥1)
B.{x|x≤1)
C.{x|x>;1)
D.{x|x≤-1或x≥1)
2.sin θ·cos θ·tan θ<0,则θ属于( )
A.(π/2,π)
B.(π,3π/2)
C.(-√2π/2,0)
D.(-π/2,0)
3.(log4 3+log8 3)(log3 2+1log9 2)=( )
A.5/3
B.7/3
C.5/4
D.1
4.圆锥的轴截面顶角是2π/3,过顶点的截面面积的最大值是4,则它的侧面积是( )
A.4√3 π
B.2√3 π
C.8π
D.8π
5.如果函数f(x)在区间[a,6]上具有单调性,且f(a)·f(b)< 0,则方程f(x)=0在区间[a,b]上( )
A.至少有一个实根
B.至多有一个实根
C.没有实根
D.必有唯一实根
6.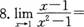 ( )
( )
A.1
B.1/2
C.O
D.∞
7.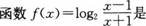 ( )
( )
A.奇函数
B.偶函数
C.既奇又偶函数
D.非奇非偶函数
8.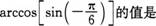 ( )
( )
A.A
B.B
C.C
D.D
9.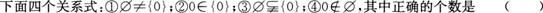
A.4
B.3
C.2
D.1
10.如果圆锥的轴截面是等边三角形,那么这个圆锥的侧面展开图的圆心角是( )
A.π
B.5π/6
C.2π/3
D.π/2
11.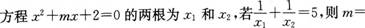 ( )
( )
A.-10
B.10
C.-5
D.5
12.8名选手在有8条跑道的运动场进行百米赛跑,其中有2名中国选手.按随机抽签方式决定选手的跑道,2名中国选手在相邻的跑道的概率为( )
A.1/2
B.1/4
C.1/8
D.1/16
13.从1,2,3,4,5,6六个数字中,选出一个偶数数字和两个奇数数字组成一个无重复数字的三位数,总共有( )
A.9个
B.24个
C.36个
D.54个
14.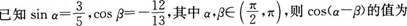 ( )
( )
A.-63/65
B.63/65
C.-33/65
D.33/65
15.若x>;2,那么下列四个式子中①x2>2x②xy>;2y;③2x>;x;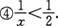 正确的有( )
正确的有( )
A.4个
B.3个
C.2个
D.1个
16.log34·log48·log8m=log416,则m为( )
A.9/2
B.9
C.18
D.27
17.在一次读书活动中,某人从5本不同的科技书和7本不同的文艺书中任选一本阅读,那么他选中文艺书的概率是( )
A.5/7
B.5/12
C.7/12
D.1/5
二、填空题:每小题4分,共16分。
18.某几何体下部是直径为2,高为4的圆柱,上部是直径为2的半球,则它的表面积为__________,体积为___________.
19.若a=(1-t,1-t,t),b=(2,t,t),则|b-a|的最小值是__________.
20.已知a=(6,2),b=(-4,1/2),直线ι过点A(3,-1),且与向量a+2b垂直,则直线ι的一般方程为__________.
21.函数f(x)=2cos2x-1的最小正周期为__________.
三、解答题:共49分。解答应写出推理、演算步骤
22.
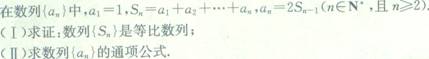
23.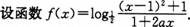 (I)求?(x)的定义域; <br>
(I)求?(x)的定义域; <br>
(Ⅱ)求使?(x)>0的所有x的值
24.已知函数?(x)=|x|,函数g(x)=| x-1 |. (Ⅰ)解不等式?(x)≥g(x); (Ⅱ)定义分段函数?(x)如下:当?(x)≥g(x)时,F(x)=?(x);当?(x)<;g(x)时,F(x)=g(x).结合(Ⅰ)的结果,试写出F(x)的解析式;(Ⅲ)对于(Ⅱ)中的函数F(x),求F(x)的最小值.
25.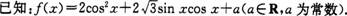
(Ⅰ)若x∈R,求?(x)的最小正周期; 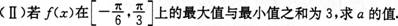
延伸阅读
成人高考微信公众号
 专注在线职业教育25年
专注在线职业教育25年
 扫描二维码
扫描二维码
 扫描二维码
扫描二维码








