2014年成人高考高起点《数学》（文史类）考前冲刺试卷（1）

2014年成人高考高起点《数学》（文史类）考前冲刺试卷（1）,本试卷总分150分，共有3类型题目。

一、选择题：本大题共17小题，每小题5分，共85分。在每小题给出的四个选项中只有一项是符合题目要求的。

1.（   ）

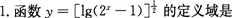A.（0，+∞）
B.（1，+∞）
C.[0，+∞）
D.[1，+∞）

2.通过点（－3，1）且与直线3x－y－3=0垂直的直线方程是（　　）

A.x+3y=0
B.3x+y=0
C.x－3y+6=0
D.3x－y－6=0

3.（   ）

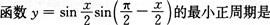A.4π
B.2π
C.π
D.π/2

4.一袋中有5个白球，3个红球，现从袋中往外取球，每次任取一个记下颜色后放回，直到红球出现10次时停止，则停止时共取12次球的概率为（　　）

A.
B.
C.
D.

5.若tan a=m且a在第三象限，则cosa的值为（　　）

A.
B.
C.
D.

6.（   ）

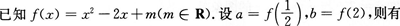A.a>b
B.a<b
C.a=b
D.a，b大小不确定

7.f（x）是定义域为R的奇函数指的是（　　）

A.f（0）=0
B.f（－3）=－f（3）
C.f（－x）+f（x）=0，x∈R
D.f（－x）=f（x），x∈R

8.在人寿保险业中，要重视某一年龄的投保人的死亡率，经过随机抽样统计，得到某城市一个投保人能活到75岁的概率为詈，则两个投保人都能活到75岁的概率为（　　）

A.9/25
B.6/25
C.3/5
D.2/5 

9.在（0，2）内是单调递增函数的是（　　）

A.y=2/x
B.y=2－x
C.y=x²－4x+5
D.y=1+x²

10.已知二次函数y=x²+ax+1在区间[1，+∞）上为递增函数，则实数a的取值范围是（　　）

A.a≥－2
B.a≤－2
C.a≥－1
D.a≤－1

11.不等式| x |≤1且x∈Z的解的个数为（　　）

A.3个
B.2个
C.0个
D.1个

12.设log₅7=a，log2₅=6，则log₂7=（　　）

A.ab^－1
B.a+b
C.2ab
D.ab

13.函数f（x）=ax³+bx+1（a，b为常数），f（2）=3，则f（－2）的值为（　　）

A.－3
B.－1
C.3
D.1

14.如果椭圆的一焦点与短轴的两个端点连线互相垂直，则这个椭圆的离心率是（　　）

A.1/2
B.√2/2 
C.√3/2  
D.1/4 

15.已知函数f（x）=1og₃（x+1）+log₃（5－x），则f（x）的（　　）

A.最大值为3
B.最大值为9
C.最大值为2
D.最小值为2

16.命题甲：直线y=b－x过原点，命题乙：b=0．则（　　）

A.甲是乙的充分条件，但不是必要条件
B.甲是乙的必要条件，但不是充分条件
C.甲既不是乙的充分条件，也不是乙的必要条件
D.甲是乙的充要条件

17.下列函数中，在区间(0，1)内为增函数的是（　　）

A.y=cos x+1
B.y=x2+1 
C.
D.

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

18.某手表厂在出厂产品中抽查100只手表，日走时误差如下：

抽查的这100只手表的平均日走时误差为________．

19.设?（x），g（x）都是定义域在（－∞，+∞）上的函数并且满足2?（x）+g（x）=x³+x²，则2?（－3）+g（3）= ________ ．

20.函数y=4x³－9x²+6x+1的驻点是________．

21.点P（7，－5）到直线5x+12y+3=0的距离是__________．

三、解答题：本大题共4小题，共49分。解答应写出推理，演算步骤。

22.（本小题满分13分）已知函数?（x）=x³+6x²．（Ⅰ）求证函数?（x）的图象经过原点，并求出?（x）在原点处的导数值；（Ⅱ）求证函数?（x）在区间[－3，－1]上是减函数

23.（本小题满分12分）求证：双曲线的一个焦点到一条渐近线的距离等于虚半轴的长．

24.（本小题满分12分）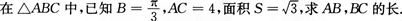

25.（本小题满分12分）