2013年成人高考高起点《数学（文）》全真模拟试卷(6)

2013年成人高考高起点《数学（文）》全真模拟试卷(6),本试卷总分150分，共有3类型题目。

一、选择题：本大题共17小题，每小题5分，共85分。在每小题给出的四个选项中只有一项是符合题目要求的。

1.函数f(x)=x²+2x- 5，则f(x-1)等于（　　）

A.x2-6
B.x2-5
C.x2-2x-6
D.x2-2x-5

2.计划在某画廊展出10幅不同的画，其中1幅水彩画，4幅油画，5幅国画，排成一横行陈列，要求同一品种的画必须排在一起，并且水彩画不放在两端，那么不同的陈列方法有（　　）

A.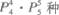
B.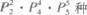
C.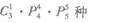
D.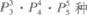

3.

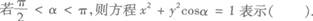
A.圆
B.椭圆
C.双曲线
D.二直线

4.已知函数f(x)=㏒2(2x+m)的定义域为[2，+∞)，则f(10)等于（　　）

A.3+㏒23
B.1+2㏒23
C.3
D.4

5.下列函数中，为奇函数的是（　　）

A.y=-x³
B.y=x³-2
C.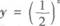
D.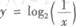

6.二次函数y=x²+4x+1的最小值是（　　）

A.1
B.-3
C.3
D.-4

7.设函数f(x)=x2+(m-3)x+3是偶函数，则m=（　　） 

A.-3
B.1
C.3
D.5

8.函数y=-x²/2+x-2的最大值是（　　）

A.-1
B.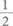
C.1
D.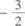

9.在△ABC中，b=7，c=5，a=4，这个三角形是（　　）

A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能推判上述结论

10.函数Y=sin2x的最小正周期是（　　）

A.6π
B.2π
C.π
D.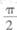

11.

A.(-∞，-4]∪[4，+∞)
B.(-∞，2] ∪[2，+∞)
C.[-4，4]
D.[-2，2]

12.经过点B(0，3)且与直线x+2y-3=0垂直的直线方程为（　　）

A.2x-y-3=0
B.y-2x-3=0
C.x+2y-6=0
D.2x+y-3=0

13.若向量a=(x，2)，b=(-2，4)，且a，b共线，则x=（　　） 

A.-4
B.-1
C.1
D.4

14.已知向量a=(3，-1)，b=(5，y)，若a∥b，则y=（　　）

A.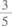
B.
C.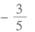
D.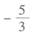

15.已知函数f(x)=㏒2(ax+b)，若f(2)=2,f(3)=3，则（　　）

A.a=1，b=-4
B.a=2，b=-2
C.a=4，b=3
D.a=4，b=-4

16.等比数列{an}中，若a1 + a2 =30，a3  + a4 =120，则a5 + a6 =（　　）

A.240
B.480
C.720
D.960

17.函数y=x²-1和y=1-x²的图像关于（　　）

A.坐标原点对称
B.x轴对称
C.y轴对称
D.直线茗+Y=0对称

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

18.二次函数y=2x²-x+1的最小值为__________．

19. 从一个班级中任取10名学生做英语口语测试，成绩如下(单位：分)
76 90 84 86 81 87 86 82 85 83
样本方差等于__________。

20.函数y=f(x)的图像平移向量a=(a₁，a₂)得到函数的图像的解析式是__________。

21.

三、解答题：本大题共4小题，共49分。解答应写出推理，演算步骤。

22. 在等比数列{a_n}中，如果a₄·a₇，=-512，a₃+ a₈=124，且公比q为整数，求a₁₀的值．

23.

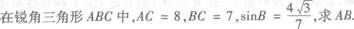
24. 求经过两圆x²+y²-2x-2y+1=0与x²+y²-6x-4y+9=0的交点，且圆心在直线y=2x上的圆的方程．

25. 设{an}为等差数列，且公差d为正数，已知a2 + a3 + a4 =15，又a2，a3-1，a4成等比数列，求a1和d