2013年成人高考高起点《数学（文）》权威预测试卷四

2013年成人高考高起点《数学（文）》权威预测试卷四：本试卷总分150分；共有3类型题目

选择题：本大题共17小题，每小题5分，共85分。在每小题给出的四个选项中只有一项是符合题目要求的。

1.
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件

2.过点(1，1)且与直线x+2y-1=0垂直的直线方程为（　　）
(A)2x-y-1=0
(B)2x-y-3=0
(C)x+2y-3=0
(D)x-2y+1=0

3.在区间(0，+∞)内是单调增函数的是（　　）
(A)y=3+x3
(B)y=3-x2
(C)y=8-x4
(D)y=-8x+1

4.从甲口袋内摸出一个球是红球的概率是0．2，从乙口袋内摸出一个球是红球的概率是0．3．现从甲、乙两个口袋内各摸出一个球，这两个球都是红球的概率是（　　）
(A)0．94
(B)0．56
(C)0．38
(D)0．06

5.已知f(2x)=x²+1，则f(1)的值为（　　）
(A)2
(B)1
(C)0
(D)3

6.设集合M={1，2，3，4，5}，集合N={2，4，6}，集合T={4，5，6}，则(M ∩ T)U N是 （　　）
(A){2，4，6}
(B){4，5，6}
(C){1，2，3，4，5，6}
(D){2，4，5，6}

7.
(A){x|x≠0，x∈R}
(B){ x|x≠±1，x∈R}
(C){ x|x≠0，x≠±1，x∈R}
(D){ x|x∈R}

8.点P(x，y)关于点a(3，-1)的对称点Q的坐标是（　　）
(A)(6-x，-2-Y)
(B)(2x-3，2y+1)
(C)(z+3，y-1)
(D)(3-x，-1-y)

9.共有8名文明乘车志愿者参加甲、乙两站的志愿服务，其中甲站需要5人，乙站需要3人，那么不同的分派方案的种数有（　　）
(A)2种
(B)28种
(C)56种
(D)336种

10.5个人站成一排照相，甲、乙两个恰好站在两边的概率是（　　）
(A)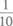
(B)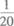
(C)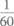
(D)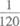

11.
(A)
(B)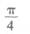
(C)
(D)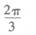

12.
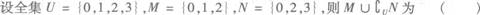
(A)空集
(B){1}
(C){0，1，2}
(D){2，3}

13.下列命题是真命题的是（　　）
(A)3>2且-1<0
(B)若A ∩ B=Φ，则A=Φ
(C)方程(x-1)2+(y+1)2=0的解是x=1或y=-1
(D)存在x∈R，使x2=-1

14.如果a，b，c成等比数列，那么ax²+2bx+c=0的根的情况是（　　）
(A)有二相等实根
(B)有二不等实根
(C)无实根
(D)无法确定

15.
(A)
(B)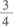
(C)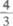
(D)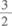

16.使sinx≤cosx成立的x的一个变化区间是（　　）
(A)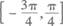
(B)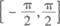
(C)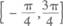
(D)[0，π]

17.
(A)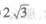
(B)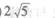
(C)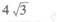
(D)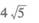

一、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

18.

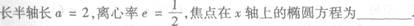
19.函数y=2cosx-cos2x的最大值是__________．

20.若函数y=x²+2(m-1)x+3m²-11的值恒为正，则实数m的取值范围是__________。

21.随机抽测某型号小包装商品6袋，测得每袋重量(单位：克)分别为
101 95 99 105 94 103
则该样本的样本方差为__________。

二、解答题：本大题共4小题，共49分。解答应写出推理，演算步骤。

22.

23.设等比数列{ a_n }的各项都是正数，其前n项和Sn=3a_n-1，求数列{ a_n }的公比q和首项a₁．

24.已知等差数列{an}中，a₁=9，a₃+ a₈=0．
(1)求数列{ a_n }的通项公式；
(2)当n为何值时，数列{ a_n}的前n项和S_n取得最大值，并求该最大值．

25.中心在原点，对称轴为坐标轴的双曲线与圆x²+y²=17交于点A(4，-1)，若该圆在A点的切线与双曲线的一条渐近线平行，求双曲线方程．