2013年成人高考高起点《数学（文）》权威预测试卷二

2013年成人高考高起点《数学（文）》权威预测试卷二：本试卷总分150分；共有3类型题目

选择题：本大题共17小题，每小题5分，共85分。在每小题给出的四个选项中只有一项是符合题目要求的。

1.
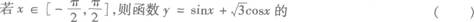
(A)最大值是1，最小值是-1
(B)最大值是1，最小值是-1/2
(C)最大值是2，最小值是-2
(D)最大值是2，最小值是-I

2.过曲线y=2x²-1上一点P(1，1)处的切线的斜率是（　　）
(A)4
(B)3
(C)1
(D)-4

3.A，B，C，D，E五人并排站成一排，如果B必须站在A的左边(A，B可以不相邻)，那么不同的排法共有（　　）
(A)24种
(B)60种
(C)90种
(D)120种

4.抛物线y=x²+x+3的焦点坐标是（　　）
(A)
(B)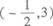
(C)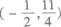
(D)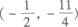

5.设集合M={x|x≥-3}，N={x|x≤1}，则 M ∩ N=（　　）
(A)R
(B)(-∞，-3]u[1，+∞)
(C)[-3，-1]
(D)φ

6.
(A)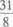
(B)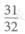
(C)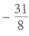
(D)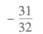

7.已知点A(-5，3)，B(3，1)，则线段AB中点的坐标为（　　）
(A)(4，-1)
(B)(-4,1)
(C)(-2，4)
(D)(-1，2)

8.sin15。cos15。=
(A)
(B)
(C)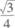
(D)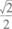

9.把6名同学排成前后两排，每排3人，则不同排法的种数是（　　）
(A)60
(B)120
(C)720
(D)1440

10.
(A)(0，+∞)
(B)(3，+∞)
(C)(0，3]
(D)(-∞，3]

11.
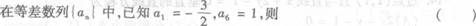
(A)a₃=0
(B)a₄=0
(C)a₅=0
(D)各项都不为0

12.
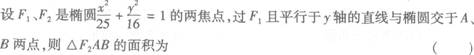
(A)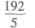
(B)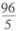
(C)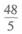
(D)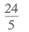

13.如果直线Y=ax+2与直线y=3x-b关于直线Y=x对称，那么（　　）
(A)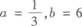
(B)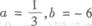
(C)a=3，6=-2
(D)a=3，b=6

14.已知数列{an}的前n项和为Sn，且S2n-1=4n2-2n+1，则Sn等于（　　）
(A)n2+n
(B)n2+n+1
(C)4n2+l
(D)4n2-2n

15.
(A)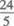
(B)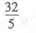
(C)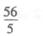
(D)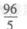

16.如果二次函数y=f(x)=3^x2-mx +4的对称轴方程为x=-5，则f(-1)=（　　）
(A)37
(B)-23
(C)22
(D)-6

17.下列函数中，函数值恒大于零的是（　　）
(A)y=x²
(B)y=2x
(C)y=㏒2x
(D)y=cosx

一、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

18.向量a=(2，5)与b=(x，-3)共线，则x=__________。

19.过直线3x+y-3=0与2x+3y+12=0的交点，且圆心在点C(1，-1)的圆的方程为__________。

20.sin275 o+sin215 o+sin75 osin15o=__________．

21.

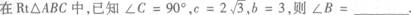
二、解答题：本大题共4小题，共49分。解答应写出推理，演算步骤。

22.火车由A站出发，经过B站开往C站，已知A、B两点相距150km，B、C两站相距180km，火车速度为60km/h，写出火车越过B站的距离y(km)与时间t(h)的函数关系
式，并求出函数的定义域与值域．

23.某工厂生产商品A，若每件定价为80元，则每年可销售80万件，政府税务部门对市场销售的商品A要征收附加税，为了增加国家收入又要利于生产发展与市场活跃，必须合理确定征税的税率，根据调查分析，当政府对商品A征收附加税为P%(即每销售100元时，应征收P元)时，则每年销售量将减少10P万件，根据上述情况，若税务部门对此商品A每年所征收的税金要求不少于96万元，求P的取值范围。

24.已知函数f(x)=x⁴+mx²+5，且f’(2)=24．
(1)求m的值；
(2)求函数f(x)在区间[-2，2]上的最大值和最小值．

25.抛物线的顶点在原点，焦点为椭圆x²+5y²=5的左焦点，过点M(-1，-1)引抛物线的弦，使M为弦的中点，求弦所在直线的方程，并求出弦长．