专升本（高等数学二）模拟试卷31

一、1.选择题

0.

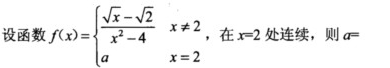
A.
B.
C.
D.

1.当x→1时，下列变量中不是无穷小量的是

A.x²-1
B.sin(x²-1)
C.lnx
D.ex-1

2.

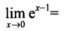
A.0
B.e^-1
C.1
D.e

3.

A.-1/4
B.-1/2
C.1/4
D.1/2

4.下列命题正确的是

A.函数f(x)的导数不存在的点，一定不是f(x)的极值点
B.若x0为函数f(x)的驻点，则x0必为f(x)的极值点
C.若函数f(x)在点x0处有极值，且f'(x0)存在，则必有f'(x0)=0
D.若函数f(x)在点XO处连续，则f'(x0)一定存在

5.

A.(-∞，0)
B.(-∞，1)
C.(0，+∞)
D.(1，+∞)

6.若f(x)的一个原函数为arctanx，则下列等式正确的是

A.∫arctanxdx=f(x)+C
B.∫f(x)dx=arctanx+C
C.∫arctanxdx=f(x)
D.∫f(x)dx=arctanx

7.

A.
B.
C.
D.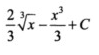

8.

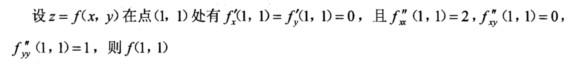
A.是极大值
B.是极小值
C.不是极大值
D.不是极小值

9.

A.对立事件
B.互不相容事件
C.
D.??

二、2.填空题

0.

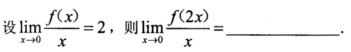
1. 设函数y=f(-x²)，且f(u)可导，则dy=________。

2. 设函数y=xⁿ+2n，则y⁽ⁿ⁾(1)=________。

3.

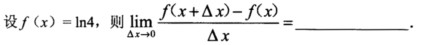
4. ∫xd(cosx)=___________。

5.

6.

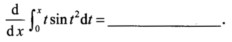
7. 设z=ulnv，而u=cosx，v=e^x，则dz/dx=__________。

8.

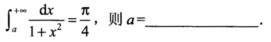
9.

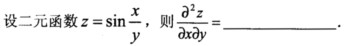
三、3.解答题

0.

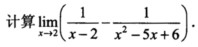
1. 设函数y=tanx/x，求y"。

2.

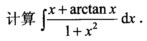
3.

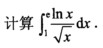
4. 某射手击中10环的概率为0．26，击中9环的概率为0．32，击中8环的概率为0．36，求在一次射击中不低于8环的概率。

5. 求函数y=ln(1+x²)的单调区间、极值、凹凸区间和拐点。

6. 求由曲线y=e^x、x²+y²=1、x=1在第一象限所围成的平面图形的面积A及此平面图形绕x轴旋转一周所得旋转体的体积V_x。

7. 设z=z(x,y)是由方程x²+2y²+xy+z²=0所确定的隐函数，求全微分dz。